Das Basismodell konnte bereits logisch denken (man musste es nur richtig fragen)

Als DeepSeek-R1 Anfang 2025 menschenähnliche Denkfähigkeiten demonstrierte, feierte die KI-Branche einen weiteren Sieg des Reinforcement Learning. Das Paradigma schien unbestreitbar: Um Modelle zu erhalten, die in der Lage sind, komplexe Probleme in Mathematik, Programmierung oder Wissenschaft zu lösen, war ein massives, auf RL basierendes Post-Training erforderlich. OpenAI mit o1, Anthropic mit Claude und sogar Open-Source-Projekte wie Qwen2.5-Math haben diesen Weg eingeschlagen: Man nehme ein Basismodell, baue ein genaues Belohnungsmodell, bereite kuratierte Datensätze mit überprüfbaren Problemen vor und trainiere dann mit Algorithmen wie GRPO (Group Relative Policy Optimization), was wochenlange Berechnungen auf GPU-Clustern erfordert.

Die Kosten dieser Orthodoxie sind beträchtlich. Wir sprechen nicht nur von Millionen von Dollar an Rechenressourcen, sondern auch von der technischen Komplexität: Hyperparameter-Sweeps zur Vermeidung von Instabilität während des Trainings, diversifizierte Datensätze, die manuell kuratiert werden müssen, und Belohnungssignale, die perfekt sein müssen, da das Modell sonst unerwünschte Verhaltensweisen lernt. Wie von Forschern von AWS und der Carnegie Mellon University dokumentiert, erfordert der RLHF-Prozess eine hochentwickelte Infrastruktur, in der Belohnungsmodell, Richtlinienoptimierung und KL-Divergenzkontrolle in einem prekären Gleichgewicht gehalten werden müssen.

Doch in den letzten Monaten sind beunruhigende Anzeichen aufgetaucht. Mehrere Veröffentlichungen haben begonnen, ein merkwürdiges Phänomen zu dokumentieren: Wenn man den pass@k (die Wahrscheinlichkeit, dass mindestens eine von k Antworten korrekt ist) von Basismodellen mit denen vergleicht, die mit RL nachgeschult wurden, gewinnen bei hohen k-Werten oft die Basismodelle. Die Forschung "Rewarding the Unlikely" von Andre He und Kollegen identifizierte das, was sie als "Rang-Bias" in GRPO bezeichnen: Der Algorithmus verstärkt bereits wahrscheinliche Trajektorien und vernachlässigt seltene, aber korrekte, was zu dem führt, was sie als "Verteilungsschärfung" bezeichnen. Das Post-RL-Modell löst einige Probleme mit weniger Stichproben, schneidet aber im Vergleich zum einfachen mehrfachen Sampling aus dem ursprünglichen Modell schlechter ab.

Es ist, als ob RL nicht wirklich neue Fähigkeiten lehrt, sondern es nur einfacher macht, die richtigen auf den ersten Versuch zu ziehen, und dabei die Vielfalt der Antworten opfert. Ein Kompromiss, der in Bereichen mit perfekten Verifizierern wie dem formalen "Beweisen von Theoremen" wie ein sehr schlechtes Geschäft erscheint.

Die Provokation aus Harvard

In diesem Kontext kommt die Forschung "Reasoning with Sampling: Your Base Model is Smarter Than You Think" von Aayush Karan und Yilun Du von der Harvard University als methodische Provokation daher. Die Frage, die sie stellen, ist radikal: Was wäre, wenn die Denkfähigkeiten bereits alle im Basismodell vorhanden wären, nur durch ineffiziente Sampling-Strategien verdeckt?

Die Intuition ist nicht neu. Wer mit Edgar Allan Poes "Der entwendete Brief" vertraut ist, wird sich daran erinnern, dass sich die Lösung manchmal direkt vor unseren Augen verbirgt, zu offensichtlich, um bemerkt zu werden. Karan und Du schlagen etwas Ähnliches vor: Anstelle von monatelangem RL-Training verwenden sie einen intelligenteren Sampling-Algorithmus, der die bereits im Basismodell enthaltenen Wahrscheinlichkeiten nutzt. Keine neuen Gewichte, kein Gradientenabstieg, kein Belohnungsmodell. Nur eine andere Art, Sequenzen aus dem bestehenden Modell zu extrahieren.

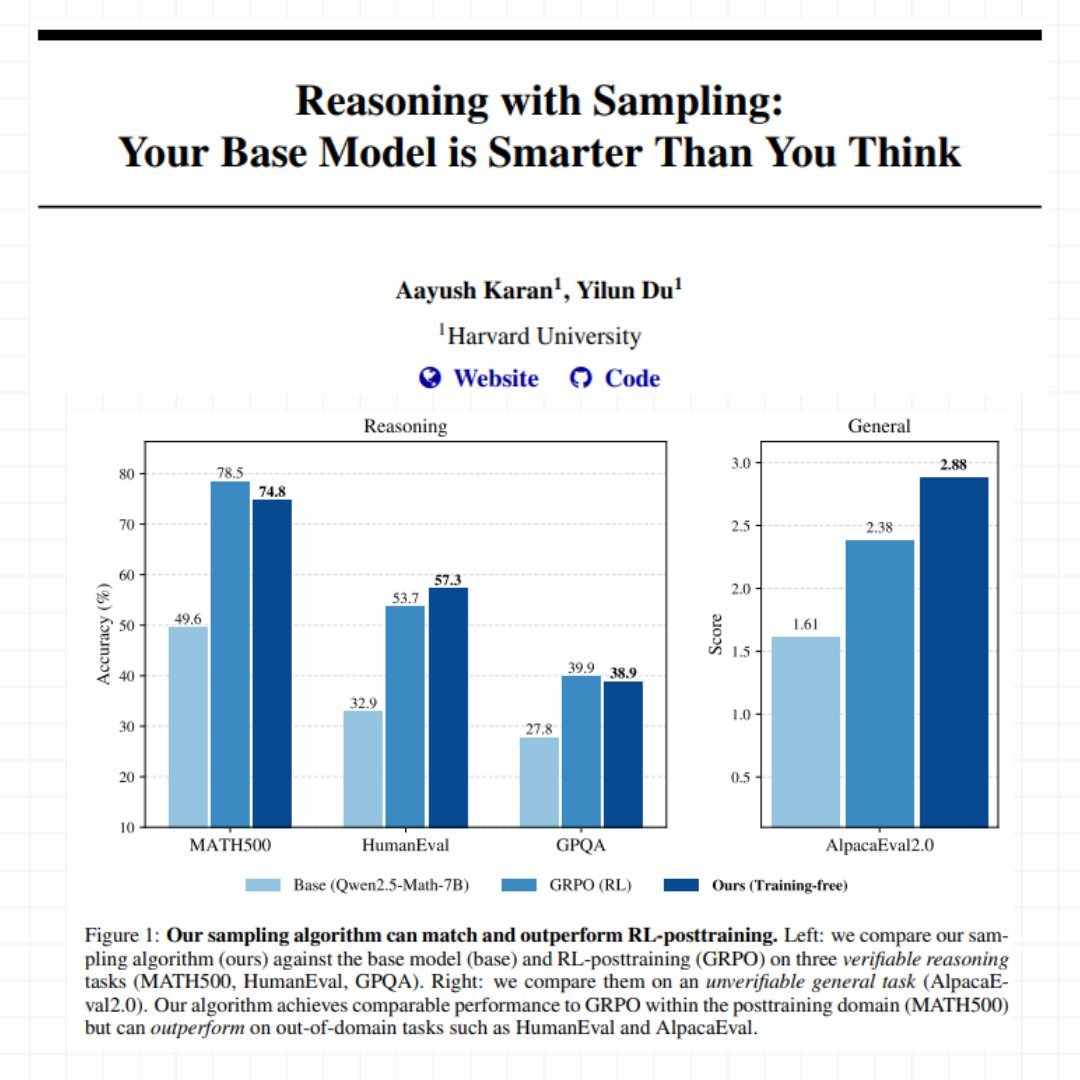
Ihre Methode heißt Power Sampling, und die Ergebnisse sind überraschend. Bei MATH500 (wettbewerbsfähige mathematische Probleme) erreicht ihr trainingsfreier Ansatz eine Genauigkeit von 74,8 % im Single-Shot mit Qwen2.5-Math-7B, was fast identisch mit den 78,5 % ist, die mit GRPO nach wochenlangem Training erzielt wurden. Aber die wahre Überraschung kommt bei Aufgaben außerhalb des Domänenbereichs: Bei HumanEval (Programmierprobleme) erzielt Power Sampling 57,3 % gegenüber 53,7 % von GRPO, und bei AlpacaEval 2.0 (allgemeine Hilfsbereitschaft) erreicht es beeindruckende 2,88 gegenüber 2,38 des nachgeschulten Modells.

Wie in den besten Moneyball-Geschichten, in denen Billy Beane entdeckte, dass statistische Effizienz millionenschwere Budgets schlägt, scheint hier der intelligente Algorithmus mit der rohen Rechenleistung zu konkurrieren. Aber wie genau funktioniert dieses Power Sampling? Bild aus dem offiziellen Harvard-Paper

Das Problem des traditionellen Samplings

Um die Innovation von Karan und Du zu verstehen, muss man zunächst verstehen, wie Sprachmodelle Text generieren. Bei jedem Schritt berechnet das Modell eine Wahrscheinlichkeit für jeden möglichen nächsten Token. Das "gierige" (greedy) Sampling wählt immer den wahrscheinlichsten, was zu einer deterministischen, aber oft repetitiven und banalen Ausgabe führt. Um Vielfalt einzuführen, verwendet die Branche seit Jahren das sogenannte "Low-Temperature-Sampling": Man modifiziert die Wahrscheinlichkeiten, um hochwahrscheinliche Auswahlmöglichkeiten noch attraktiver zu machen, als würde man einen Thermostat einstellen, der steuert, wie viel Risiko das Modell eingehen will.

Das Problem ist, dass dieser Ansatz nur den nächsten Token betrachtet und völlig ignoriert, was in den folgenden Schritten passieren wird. Es ist, als würde man entscheiden, welchen Weg man einschlägt, indem man nur den ersten Meter betrachtet: Vielleicht führt der Weg, der am Anfang schöner aussieht, in eine Sackgasse, während der unscheinbarere auf eine Autobahn mündet.

Die Harvard-Forscher erklären das Phänomen mit einer aufschlussreichen Analogie. Stellen Sie sich vor, Sie müssten zwischen zwei Token wählen. Der erste hat viele mögliche Fortsetzungen, die alle mittelmäßig sind. Der zweite hat nur sehr wenige, aber eine davon ist ausgezeichnet. Das traditionelle Low-Temperature-Sampling neigt dazu, den ersten zu bevorzugen, weil seine Fortsetzungen "im Durchschnitt" eine anständige Wahrscheinlichkeit zu haben scheinen. Aber man wettet auf Quantität statt auf Qualität.

Dies hängt direkt mit dem zusammen, was neuere Veröffentlichungen als "kritische Fenster" oder "zentrale Token" bezeichnen: Momente in der Generierung, in denen ein einziger falscher Token das Modell in eine zum Scheitern verurteilte Trajektorie einsperrt. Forscher wie Li, Karan und Chen haben dokumentiert, wie diese kritischen Punkte stark mit Denkfehlern korrelieren. Das Modell hatte die richtige Antwort in seinen internen Wahrscheinlichkeiten, aber die Sampling-Methode hat es auf den falschen Weg geführt.

Power Sampling: Ein Blick in die Zukunft

Die von Harvard vorgeschlagene Lösung heißt "Power Distribution" und ist konzeptionell elegant: Anstatt nur den nächsten Token zu betrachten, berücksichtigt sie explizit die Wahrscheinlichkeit ganzer zukünftiger Sequenzen. In der Praxis fragt das Modell nicht mehr "welcher Token ist jetzt am wahrscheinlichsten?", sondern "welcher Token führt mich zu den wahrscheinlichsten vollständigen Sequenzen?".

Der Unterschied scheint subtil, ist aber tiefgreifend. Kehren wir zum Beispiel der Gabelung zurück: Mit der traditionellen Methode, wenn der erste Token zu zehn mittelmäßigen Wegen führt (sagen wir, jeder mit 5 % Wahrscheinlichkeit), sieht das Modell insgesamt 50 % und findet das attraktiv. Der zweite Token führt nur zu zwei Wegen, aber einer hat eine Wahrscheinlichkeit von 40 %. Die traditionelle Methode bevorzugt den ersten. Power Sampling hingegen betrachtet den bestmöglichen Weg von jeder Gabelung und sagt: "Der zweite Token kann mich zu einer Sequenz mit 40 % Wahrscheinlichkeit führen, der erste höchstens zu 5 %. Ich nehme den zweiten."

Dieser Ansatz löst das Problem der zentralen Token auf natürliche Weise. Wenn das Modell an einen dieser kritischen Momente gelangt, an denen eine Wahl es einsperrt und die andere es befreit, neigt Power Sampling dazu, die befreiende zu wählen, da es explizit die langfristigen Konsequenzen betrachtet.

Aber es gibt ein nicht triviales technisches Problem: Um die Wahrscheinlichkeiten aller möglichen zukünftigen Sequenzen zu berechnen, wären astronomische Berechnungen erforderlich. Mit einem Vokabular von fünfzigtausend Token und Sequenzen von tausend Token sprechen wir von 50000^1000 zu bewertenden Möglichkeiten. Das ist buchstäblich unmöglich.

MCMC: Monte Carlo rettet die Situation

Hier kommt ein Stück Geschichte der computergestützten Statistik aus den 1950er Jahren ins Spiel. Der Metropolis-Hastings-Algorithmus, ursprünglich 1953 von einem Team von Physikern am Los Alamos National Laboratory zur Simulation von Atomsystemen vorgeschlagen, löst genau diese Art von Problem: Wie man aus einer Verteilung sampelt, wenn es unmöglich ist, sie direkt zu berechnen.

Die Idee ist genial. Anstatt alles zu berechnen, baut man einen "intelligenten Zufallsweg" durch den Raum der Möglichkeiten. Man beginnt mit einer beliebigen Sequenz. Man schlägt eine zufällige Änderung vor (z. B. einen Teil der Sequenz neu generieren). Dann vergleicht man die Wahrscheinlichkeit der neuen Version mit der alten. Wenn die neue besser ist, akzeptiert man sie. Wenn sie schlechter ist, akzeptiert man sie trotzdem mit einer gewissen Wahrscheinlichkeit, die davon abhängt, wie viel schlechter sie ist. Man wiederholt diesen Prozess viele Male.

Das Schöne daran ist, dass man keine absoluten Wahrscheinlichkeiten berechnen muss, sondern nur relative: neu vs. alt. Und das können Sprachmodelle sehr gut, denn genau das tun sie bei der normalen Inferenz. Die mathematische Magie von Metropolis-Hastings garantiert, dass, wenn man diesen Prozess oft genug wiederholt, der "Zufallsweg" konvergiert und genau aus der gewünschten Verteilung sampelt.

Karan und Du implementieren eine spezifische Variante für Sprachmodelle. Bei jedem Schritt des Algorithmus wählen sie zufällig einen Punkt in der Sequenz und generieren alles von dort an neu. Dann vergleichen sie die Gesamtwahrscheinlichkeit der neuen Sequenz mit der alten (immer unter Verwendung des Basismodells) und entscheiden, ob sie die neue Version behalten oder bei der alten bleiben. Der Prozess wird für jeden generierten Text-"Block" mehrmals wiederholt.

Es ist wie ein Bildhauer, der Stein bearbeitet: Er beginnt mit einer groben Form und verfeinert sie nach und nach mit strategischen Schlägen, akzeptiert Verbesserungen und toleriert gelegentlich kleine Rückschritte, um nicht stecken zu bleiben. Jeder "Schlag" kostet eine teilweise Neugenerierung des Textes, aber das Endergebnis ist eine Sequenz, die aus der gewünschten Verteilung sampelt.

Die Zahlen, die das Blatt wenden

Die Benchmarks lügen nicht. Bei drei verschiedenen Modellen (Qwen2.5-Math-7B, Qwen2.5-7B und Phi-3.5-mini-instruct) erzielt Power Sampling enorme Steigerungen im Vergleich zu den Basismodellen. Wir sprechen von Verbesserungen von 25 % bei MATH500 mit Qwen2.5-Math und sogar 52 % bei HumanEval mit Phi-3.5-mini. Aber der interessanteste Vergleich ist mit GRPO, der als State-of-the-Art geltenden RL-Methode.

Bei MATH500, dem Bereich, in dem GRPO trainiert wurde (es hat buchstäblich Tausende ähnlicher mathematischer Probleme während des Trainings gesehen), kommt Power Sampling sehr nahe: 74,8 % gegenüber 78,5 %. Eine Lücke von 3,7 % ist nicht zu vernachlässigen, aber man muss den Kontext berücksichtigen: GRPO erforderte tagelanges Training auf einem GPU-Cluster, Hyperparameter-Optimierung und kuratierte Datensätze. Power Sampling arbeitet auf einem vollständig eingefrorenen Modell, ohne jemals ein Gewicht anzufassen.

Die wahre Offenbarung kommt jedoch, wenn man den Trainingsbereich verlässt. Bei HumanEval, einem Benchmark für Programmierprobleme, erzielt Power Sampling mit Qwen2.5-Math 57,3 % gegenüber 53,7 % von GRPO. Es schlägt das auf Mathematik spezialisierte Modell bei Programmierproblemen. Bei AlpacaEval 2.0, das misst, wie hilfreich das Modell in allgemeinen Gesprächen ist (ohne Möglichkeit zur automatischen Überprüfung), erreicht Power Sampling 2,88 gegenüber 2,38 von GRPO, ein Vorteil von 21 %.

Mit Phi-3.5-mini wird die Lücke dramatisch: 73,2 % gegenüber 13,4 % bei HumanEval. Das ist kein Tippfehler: Das mit RL nachgeschulte Modell bricht bei einer Aufgabe außerhalb seines Trainingssatzes zusammen, während Power Sampling eine hervorragende Leistung beibehält.

Aber die vielleicht aufschlussreichste Angabe ist die Grafik des pass@k, d.h. wie oft mindestens eine von k Antworten korrekt ist. GRPO zeigt das klassische Problem des "Diversitätskollaps": Der pass@16 ist nur geringfügig höher als der pass@1, ein Zeichen dafür, dass das Modell immer sehr ähnliche Antworten generiert. Power Sampling hingegen behält eine stetig steigende Kurve bei, die sich allmählich der Obergrenze des Basismodells nähert. In der Praxis: Es erzielt eine Single-Shot-Leistung, die mit GRPO vergleichbar ist, behält aber die Fähigkeit des ursprünglichen Modells bei, verschiedene Lösungen zu erkunden.

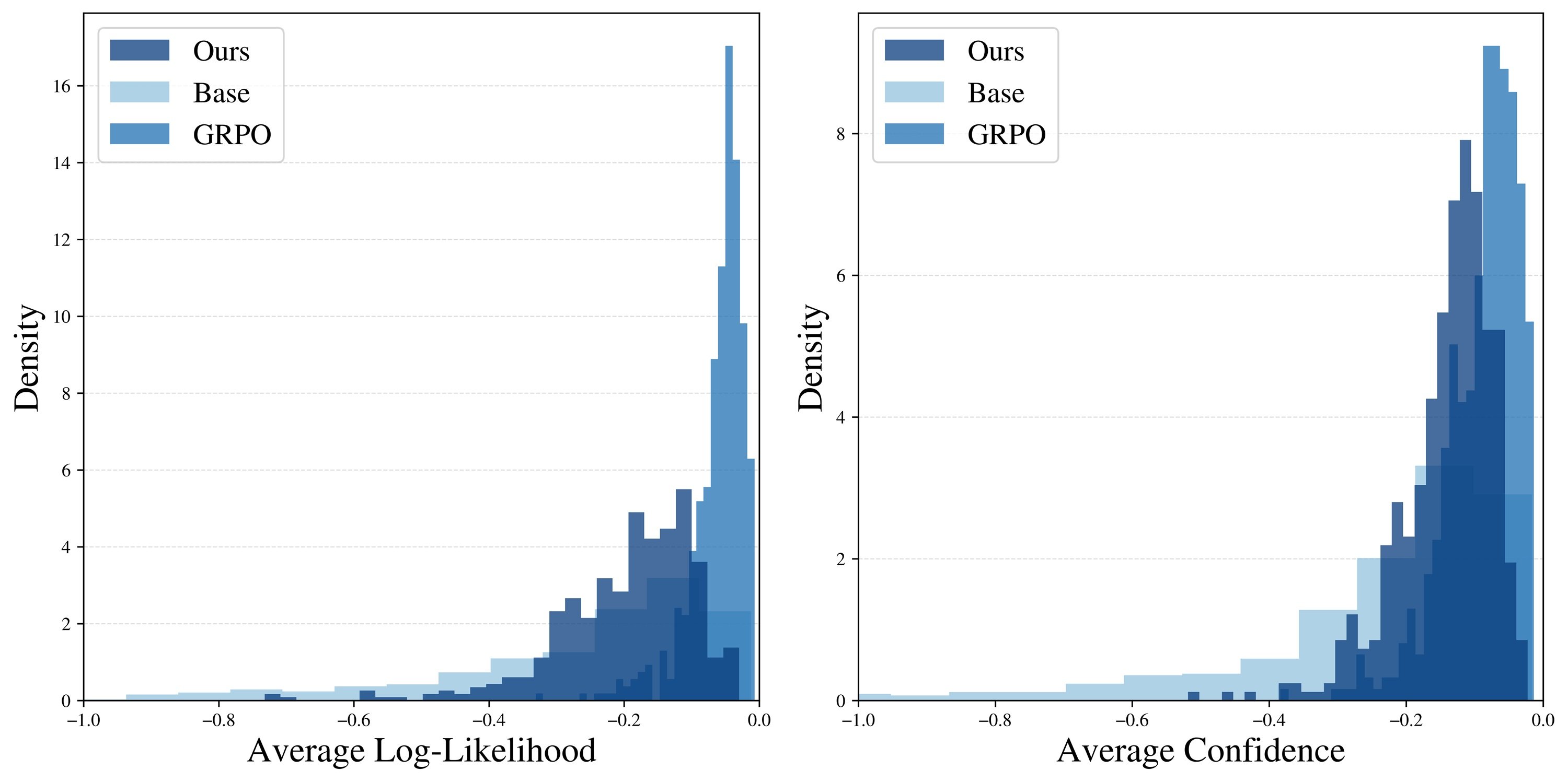
Eine tiefere Analyse bestätigt die Intuition. Wenn die Forscher messen, wie "wahrscheinlich" die generierten Antworten sind (laut Basismodell), stellen sie fest, dass GRPO einen sehr schmalen Gipfel bei den Sequenzen mit sehr hoher Wahrscheinlichkeit erzeugt. Es ist, als hätte es ein bestimmtes Rezept gelernt und wiederholt es zwanghaft. Power Sampling hingegen verteilt seine Antworten über einen breiteren Bereich wahrscheinlicher Sequenzen und behält die Vielfalt bei, ohne die Qualität zu opfern.

Ein merkwürdiges Phänomen: Die Antworten von Power Sampling sind im Durchschnitt so lang wie die von GRPO (etwa 679 Token gegenüber 671 bei MATH500), obwohl der Algorithmus lange Sequenzen nicht explizit fördert. Das "erweiterte Denken" entsteht auf natürliche Weise, wahrscheinlich weil artikuliertere und detailliertere Denkwege dazu neigen, im Basismodell höhere zusammengesetzte Wahrscheinlichkeiten zu haben. Bild aus dem offiziellen Harvard-Paper

Die Kosten des intelligenten Denkens

Natürlich ist nichts umsonst. Power Sampling erfordert mehr Rechenleistung während der Inferenz. Die Forscher schätzen, dass die Generierung einer Antwort mit den in ihren Experimenten verwendeten Parametern etwa 8,84-mal mehr Token erfordert als eine Standardgenerierung. Das liegt daran, dass der Algorithmus im MCMC-"Verfeinerungs"-Prozess wiederholt Teile der Sequenz neu generiert.

Um das ins rechte Licht zu rücken: Eine GRPO-Trainingsepoche mit Standardkonfiguration kostet immer noch mehr, da sie für jedes Beispiel mehrere Rollouts generieren und einen größeren Datensatz verwalten muss. Aber es gibt einen grundlegenden Unterschied: Die Kosten für GRPO sind einmalig (man zahlt einmal, dann ist das Modell schneller), während Power Sampling die Kosten bei jeder Inferenz bezahlt.

Es gibt jedoch auch eine andere Seite der Medaille. GRPO benötigt leistungsstarke GPUs mit viel Speicher, um Modellgewichte, Optimiererzustände im RAM zu halten und KL-Strafen zu berechnen. Power Sampling kann auf günstigerer, für Inferenz optimierter Hardware laufen, da es die Gewichte nie ändert. Und vor allem: Es funktioniert auf jedem Basismodell, ohne dass kuratierte Datensätze, perfekte Belohnungssignale oder wochenlanges Trainings-Babysitting erforderlich sind.

Die Experimente zeigen auch, dass der Algorithmus überraschend robust ist. Der Hauptparameter, der abgestimmt werden muss (im Paper Alpha genannt), funktioniert in einem weiten Bereich gut: Jeder Wert zwischen 2 und 6 liefert vergleichbare Ergebnisse für mathematische Aufgaben. Die Anzahl der erforderlichen MCMC-Schritte ist bescheiden: Bereits mit 2 Schritten sind erhebliche Verbesserungen zu sehen, und 10 Schritte scheinen für die Konvergenz auszureichen. Mehr bringt kaum etwas.

Dies deutet darauf hin, dass der Algorithmus den Raum der möglichen Sequenzen effektiv "mischt" und die typischen Pathologien von MCMC in hohen Dimensionen vermeidet, wo Millionen von Iterationen zur Konvergenz erforderlich wären. Es ist ein Zeichen dafür, dass die theoretische Intuition in eine funktionierende praktische Algorithmik umgesetzt wird.

Implikationen und offene Fragen

Es gibt jedoch Einschränkungen, und es ist wichtig, sie anzuerkennen. Erstens handelt es sich um eine vorläufige Forschung: Die Skalierung zur Testzeit ist noch weitgehend unerforschtes Gebiet. Wir wissen nicht, wie sich Power Sampling in langen, mehrstufigen Gesprächen oder bei Aufgaben verhält, die ein erweitertes kontextuelles Gedächtnis erfordern. Für Bereiche, in denen die Überprüfung teuer oder unmöglich ist (wie kreatives Schreiben oder subjektive Zusammenfassungen), wird die Messung der Vorteile viel nuancierter.

Dann gibt es einen tieferen epistemologischen Aspekt, den das Paper nur am Rande berührt: Wenn Power Sampling so gut funktioniert, was sagt uns das wirklich über Reinforcement Learning? Eine optimistische Antwort ist, dass RL und Power Sampling komplementäre Signale erfassen: Vielleicht lehrt RL tatsächlich neue Denkmuster, die während des Trainings entstehen, während Power Sampling besser darin ist, bereits latente Fähigkeiten zu extrahieren.

Aber die provokantere Interpretation ist, dass ein Großteil des Gewinns durch RL eine "teure Verteilungsschärfung" ist, die mit "billigem Sampling" repliziert werden kann. Wenn das der Fall ist, müssten die Skalierungskurven neu interpretiert werden. Nicht mehr "wie viel RL wird für eine X%ige Steigerung benötigt", sondern "wie viel Gewinn bietet RL über die Obergrenze des Basismodells mit optimalem Sampling hinaus".

Diese Perspektive knüpft direkt an unsere früheren Artikel über Samsungs TRM und Microsofts DeepConf an, in denen wir untersucht haben, wie intelligente algorithmische Strategien wettbewerbsfähige Ergebnisse erzielen können, ohne auf rohe Skalierung zurückzugreifen. TRM nutzte die Abfrage zur Testzeit, um die Faktizität zu verbessern, DeepConf nutzte das intrinsische Vertrauen zur Selbstkorrektur, und Power Sampling extrahiert das Denken aus den Basiswahrscheinlichkeiten. Der rote Faden ist klar: Die künstliche Intelligenz von 2025 entdeckt wieder, dass das Problem manchmal nicht die Größe des Modells ist, sondern wie man es verwendet.

Dann gibt es die praktische Frage der Einführung. Power Sampling erfordert erhebliche Änderungen an der Inferenz-Infrastruktur: Anstelle eines einfachen Vorwärtsdurchlaufs muss die MCMC-Schleife mit Akzeptanz/Ablehnung implementiert werden. Sollten API-Anbieter dies als Option anbieten? Zu welchem Preis? Wie kann man die vom Benutzer wahrgenommene Latenz (die zunimmt) mit der Qualität der Antwort ausgleichen?

Und es gibt interessante Wettbewerbsimplikationen. Open-Source-Modelle könnten Power Sampling nutzen, um mit größeren proprietären Modellen zu konkurrieren, ohne teure Nachschulungen zu benötigen. Aber die proprietären Anbieter könnten die beiden Ansätze kombinieren: RL-Training plus Power Sampling bei der Inferenz, um das Beste aus beiden Welten zu erhalten. Wer in diesem Rennen gewinnt, wird davon abhängen, wie schnell sich das Ökosystem anpasst.

In einer Branche, die von "größer ist besser" und "mehr Training ist besser" besessen ist, sind Forschungen wie diese aus Harvard eine gesunde Erinnerung daran, dass algorithmische Innovation mindestens genauso wichtig ist wie die Skalierung. Nicht um die Skalierung zu ersetzen (die entscheidend bleibt), sondern um die Grenzen der Effizienz zu erkunden, wo jeder Token kostet und jede Idee den Unterschied zwischen nachhaltigen und nicht nachhaltigen Systemen ausmachen kann.

Wie jeder Ingenieur, der mit Ghost in the Shell aufgewachsen ist, sagen würde, entdecken wir manchmal, dass die Seele bereits in der Maschine war. Wir mussten nur lernen, sie richtig zu rufen. Die Frage ist nun: Wie viele andere latente Fähigkeiten verbergen sich in unseren Basismodellen und warten darauf, dass jemand den richtigen Algorithmus erfindet, um sie zu extrahieren?